حل معادلات دیفرانسیل در سیمولینک – سیمولینک متلب یکی از بهترین ابزار ها برای شبیه سازی و حل بسیاری از مسائل ریاضی و مهندسی است. با استفاده از سیمولینک، می توانیم بدون کدنویسی و صرفا با اتصال بلوک ها به یکدیگر، مسئله مورد نظرمان را حل کنیم.
در این بخش قصد داریم به نحوه حل معادلات دیفرانسیل در سیمولینک بپردازیم.
سایر آموزش های مرتبط با متلب و سیمولینک را هم در این بخش ببینید!
فرض کنید قصد داریم پاسخ معادله زیر را به دست آوریم:
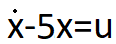
U ثابت و نامتغیر با زمان
در گام اول فرض می کنیم ورودی مقدار ثابت و برابر 1 دارد یعنی u=1 .
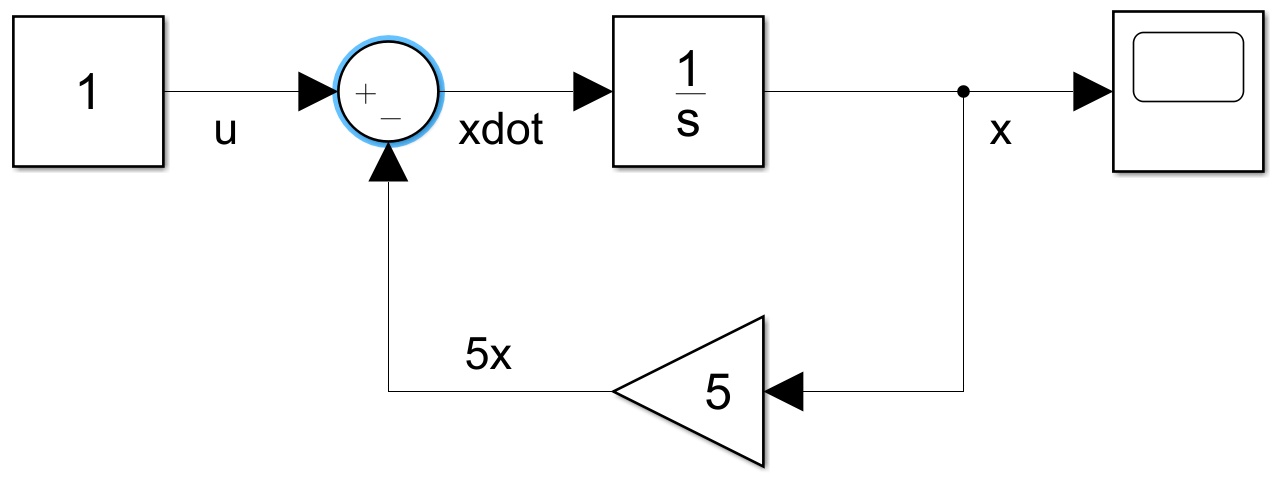
با اتصال بلوک ها به صورت زیر می توانیم پاسخ این معادله را به دست آوریم.
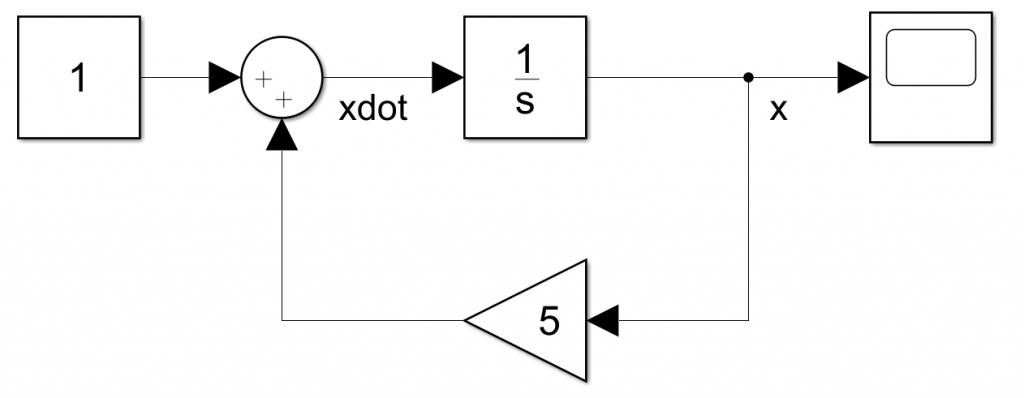
در نگاه اول شاید کمی سخت به نظر بیاید! اما اگر معادله را به صورت زیر بازنویسی کنیم، احتمالا بهتر متوجه خواهید شد:
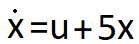
بلوک هایی که در این پروژه استفاده کرده ایم، به شرح زیر هستند:
بلوک constant: برای ایجاد یک ورودی که مقدار ثابت داشته باشد، از این بلوک استفاده کردیم. می توانیم اعداد ثابت دیگر را به جای 1 هم وارد نماییم.
بلوک sum: مقدار ورودی را با 2x جمع می کند تا سمت راست تساوی ایجاد شود.
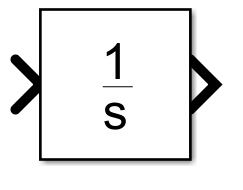بلوک integrator: از سیگنال ورودی خودش یعنی xdot انتگرال می گیرد تا خروجی x را ایجاد کند.
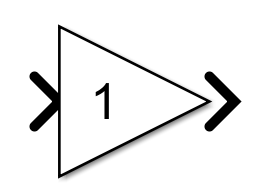بلوک gain: مقدار ورودی اش یعنی x را در یک عدد ( در این پروژه عدد 5 ضرب می کند.)
بلوک scope: بعد از run گرفتن از پروژه، با دوبار کلیک روی این بلوک، نمودار پاسخ ورودی اش را (یعنی x) بر حسب زمان رسم می کند.
اگر از پروژه run بگیریم و روی بلوک scope دوبار کلیک کنیم، پاسخ معادله (x) بر حسب زمان نمایش داده می شود. همانطور که مشاهده می کنید این پاسخ ناپایدار است و به سمت بی نهایت میل میکند.
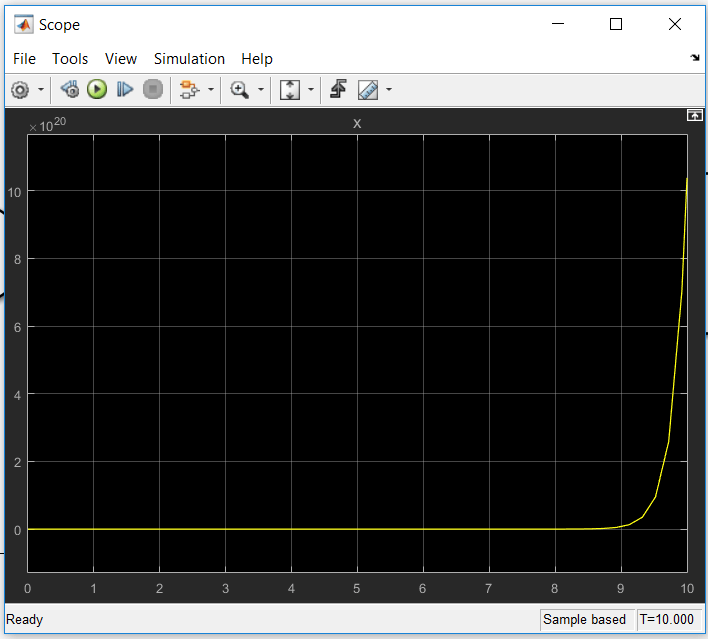
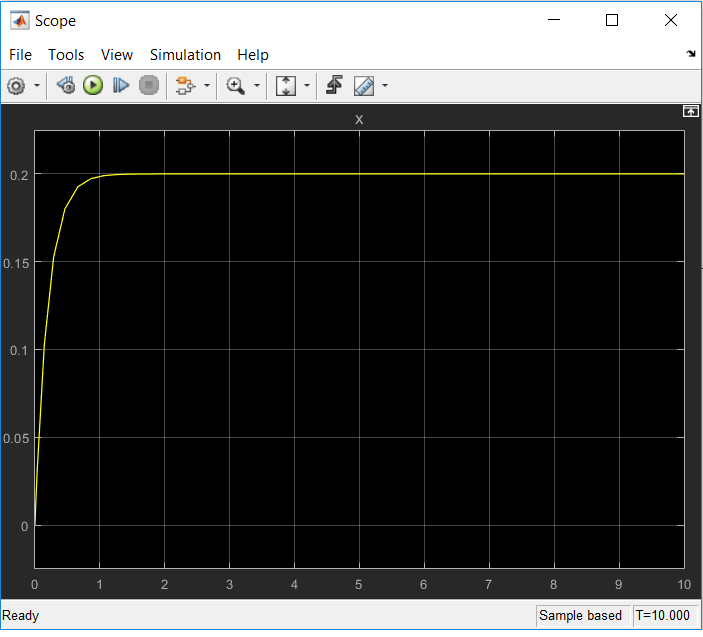
با تغییر زیر، پاسخ x پایدار خواهد شد:
مشاهده می کنید که در نمودار زیر پاسخ x پایدار شده است.
U متغیر با زمان
می خواهیم معادله زیر را حل کنیم.
در این حالت فرض می کنیم مقدار u برابر 2t باشد و با زمان تغییر کند. در این حالت کافیست که فقط به جای بلوک constant از بلوک clock که به ما مقدار t را در هر لحظه به ما می دهد استفاده کنیم. بعد از بلوک clock به یک بلوک gain هم نیاز داریم تا ضریب 2 را برای u=2t ایجاد کنیم.
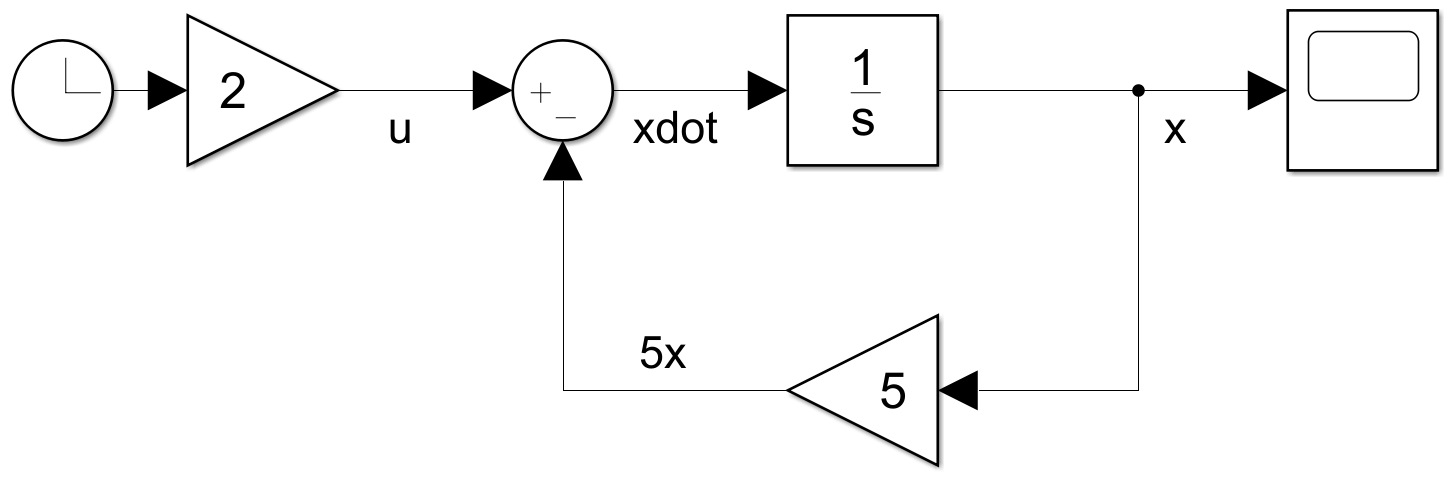
حالا پروژه آماده است. پس از run گرفتن، با دو بار کلیک روی بلوک scope می توانیم نمودار زیر را مشاهده کنیم.
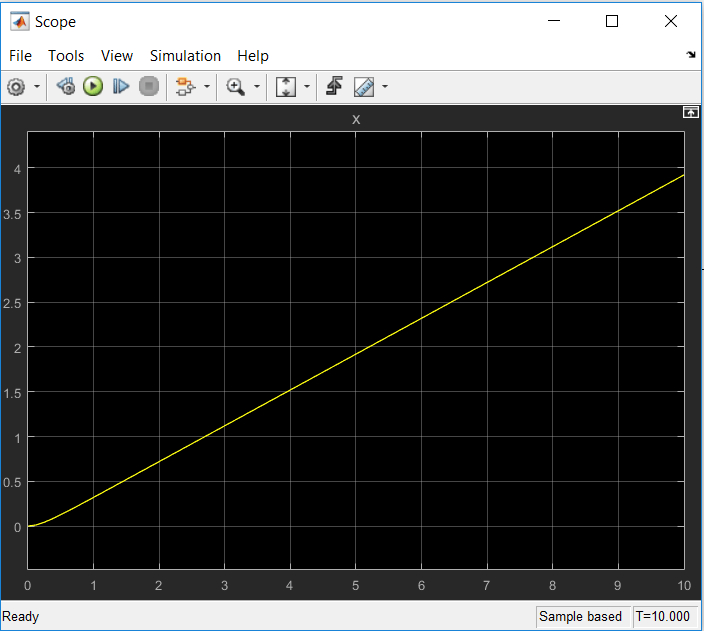
همان طور که مشخص است، پاسخ x در این حالت به سمت بی نهایت میل می کند و ناپایدار است. این به دلیل نوع ورودی 2t است که خودش هم در زمان بی نهایت به سمت بی نهایت می رود.
در این بخش با حل معادلات دیفرانسیل در سیمولینک آشنا شدیم.
در بخش های دیگر حل معادلات با مرتبه های بالاتر را هم بررسی خواهیم کرد.
لینک های مفید:
سایت رسمی MathWorks شرکت سازنده نرم افزار متلب
