یکی از مهم ترین مفاهیمی که در نرم افزار آباکوس با آن مواجه می شویم، حلگرهای Implicit و Explicit هستند.

معمولا برای کسانیکه به تازگی کار با آباکوس را شروع کرده اند، تشخیص این که در هر مسئله از بین این دو حلگر، کدام یک را باید انتخاب کنند کار دشواری است.

در این مقاله سعی کرده ایم با زبانی ساده، مفهوم هر یک از این حلگرها را بررسی کنیم. خواهیم دید که در مواجهه با انواع مسائلی که در برابر ما قرار می گیرد، چگونه باید تصمیم گیری نهایی برای انتخاب حلگر در آباکوس را انجام دهیم.

تفاوت روش Implicit و Explicit چیست؟

تفاوت این دو روش، به الگوریتم هایی مربوط می شود که هر روش برای گام زمانی (Time Incrementation) به کار می گیرد.

به صورت کلی، در هر دو روش، حالت سیستم و مدل ما در چند نقطه در طول زمان مشخص t محاسبه می شود. حالت مدل در هر نقطه، بر اساس حالت آن در نقطه قبلی محاسبه می شود. (منظور از نقطه، یک لحظه زمانی است. مثلا محاسبات مربوط به سیستم در لحظات 0.2 و 0.5 و 0.7 و1 در طول مدت 1 ثانیه شبیه سازی، انجام شده است. اصطلاحا می گوییم که محاسبات در این نقطه ها انجام شده است.)

در روش Explicit حالت سیستم در نقطه بعدی، می تواند مستقیما بر اساس اطلاعات حالت سیستم در نقطه کنونی محاسبه شود. در واقع این کار با استفاده از برون یابی انجام می شود.

بر خلاف روش Explicit ، در روش Implicit محاسبه حالت سیستم در نقطه بعدی با توجه به اطلاعات فعلی قابل انجام نیست. بلکه سیستمی از معادلات باید حل شود تا پاسخ ها به دست بیایند. برای حل این معادلات به یک الگوریتم حل غیر خطی نیاز داریم که معمولا از الگوریتم نیوتون-رافسون استفاده می کنیم.

در روش Explicit محاسبات در هر گام سختی چندانی ندارد. چون همه اطلاعات مورد نیاز فراهم است و محاسبات به سرعت انجام می شود. اما نکته مهم اینجاست که ما نمی توانیم طول هر بازه زمانی (یعنی فاصله نقاط مشخص شده) را زیاد کنیم. بزرگ شدن گام های زمانی در حل به روش Explicit در آباکوس، می تواند منجر به ناپایدار شدن حل شود.

چرا؟ همان طور که اشاره کردیم، اساس محاسبه در روش Explicit در آباکوس، برون یابی است. وقتی بازه بزرگ شود، خطای این برون یابی افزایش می یابد.

چون در برون یابی، اطلاعات یک نقطه را در خارج از بازه ای که به آن احاطه و دانش داریم محاسبه می کنیم. حالا وقتی فاصله نقطه فوق از نقطه ای که اطلاعات آن را داریم زیاد شود، طبیعتا خطا هم افزایش می یابد.

 وقتی خطای ایجاد شده در گام های زمانی با یکدیگر جمع شوند، یک خطای بزرگ ایجاد می شود که به صورت نمایی رشد می کند. در نتیجه مسئله را ناپایدار می کند.

آباکوس به صورت خودکار، بزرگترین گام زمانی که می تواند از ناپایدار شدن مسئله جلوگیری کند (در واقع کوچک ترین گام پایدار!) را محاسبه می کند و به کاربر پیشنهاد می دهد. (Stable Time Increment)

این «کوچکترین گام زمانی پایدار» یا Stable Time Increment همیشه ثابت نیست و با توجه به اطلاعات پروژه می تواند تغییر کند. اگر سایز و اندازه المان کوچک شود، کوچکترین گام زمانی پایدار هم کوچک می شود. (یعنی وقتی المان کوچک می شود، برای پایداری باید گام زمانی را هم کوچکتر کنیم.)

همچنین با کم شدن چگالی یا زیاد شدن سفتی هم اندازه این گام زمانی کوچکتر می شود.

اما یک سوال: در یک قطعه بزرگ که مش زده شده، المان هایی با اندازه های متفاوت موجود است. گام زمانی پایدار در این حالت با توجه به کدام المان تعیین می شود؟

در این حالت کوچکترین المان در نظر گرفته می شود و گام زمانی پایدار با توجه به آن تعیین می شود. به همین دلیل است که اگر حتی یک المان بدشکل یا خیلی کوچک در مدل وجود داشته باشد، می تواند تاثیر خیلی بزرگ و بدی روی کل شبیه سازی بگذارد و زمان شبیه سازی را به شدت طولانی تر کند.

گام زمانی پایدار معمولا در طول حل ثابت باقی می ماند به همین خاطر با تمام شدن اولین گام، می توانیم زمان کل شبیه سازی را به صورت حدودی تخمین بزنیم.

حجم محاسبات در یک گام زمانی در روش Implicit بسیار بیشتر است. چون همان طور که گفتیم یک دستگاه از معادلات باید حل شود. برای تحلیل های غیرخطی، حتی این کار باید چند بار انجام شود. به همین خاطر برای محاسبات مربوط به یک گام زمانی Implicit حافظه بیشتری از کامپیوتر نیاز است و زمان بیشتری هم طول می کشد.

اما از طرف دیگر، در روش Implicit محدودیت شدیدی برای اندازه گام زمانی نداریم. با توجه به اینکه در این روش محاسبات به شیوه نیوتون – رافسون و از طریق تکرار و اصلاح انجام می شود، با بزرگ شدن گام زمانی هم می توانیم به پاسخ صحیح برسیم.

هر چه مساله پیچیده تر باشد، در روش نیوتون – رافسون برای همگرا شدن مساله (Converging) به محاسبات و تکرار بیشتری نیاز است. آباکوس با در نظر گرفتن این موضوع، در Abaqus\Standard (حلگر Implicit) یک گام زمانی بهینه به صورت خودکار پیشنهاد می دهد که می تواند بسیار مفید و کمک کننده باشد.

به تصاویر زیر دقت کنید.

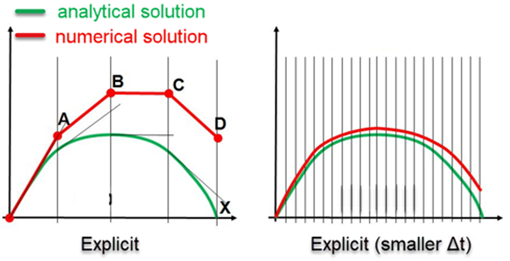
در نمودارهای بالا، پاسخ دقیق که با استفاده از روش تحلیلی به دست می آید مشخص شده است. همچنین تابعی که از روش عددی و با حلگر Explicit به دست آمده را با رنگ قرمز مشاهده می کنیم.

همان طور که کاملا مشخص است، در نمودار سمت راست که گام های زمانی نسبت به نمودار سمت چپ کوچک تر شده است، پاسخ به دست آمده هم به پاسخ اصلی بسیار نزدیک تر است.

همان طور که گفتیم در این روش با بزرگ شدن گام زمانی دقت پایین می آید، خطا زیاد می شود و حتی ممکن است مسئله ناپایدار شود.

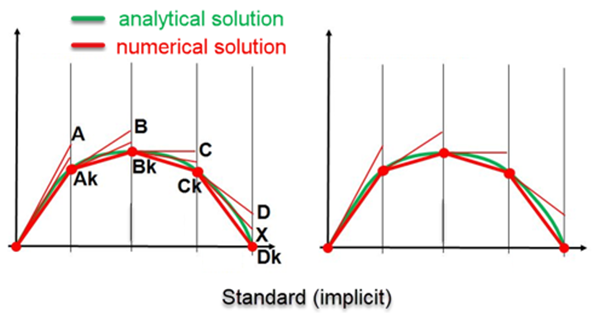
تصویر بالا، مقایسه حل عددی با استفاده از حلگر Implicit و حل دقیق و تحلیلی را ارائه می دهد. همان طور که مشخص است، با وجود بزرگ بودن گام های زمانی، باز هم پاسخ به دست آمده از روش عددی، دقت بالایی دارد. دلیل این دقت بالا، استفاده از فرایند تکرار در روش نیوتون رافسون است.

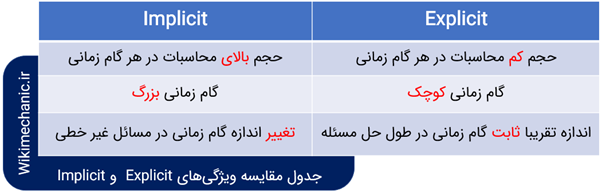
خب اجازه بدهید تا اینجای کار بحث را به صورت خیلی خلاصه در یک جدول با هم مرور کنیم:

اثرات دینامیکی

حلگر Implicit (Abaqus\Standard) می تواند برای حل مسائلی که تعادل استاتیکی دارند، به کار گرفته شود. یعنی مسائلی که در آنها جمع برداری نیروهای وارد شده برابر با صفر است.

همچنین اثرات دینامیکی هم ممکن است به مسئله افزوده شود. اگر اثرات دینامیکی در مسئله وجود نداشته باشد، یک تعادل استاتیکی باید وجود داشته باشد.

 اینرسی منجر به پایداری سیستم نمی شود در نتیجه حرکت به صورت جسم صلب، امکان پذیر نیست: پس همه پارت ها باید در همه جهات ها به زمین متصل شده باشند.  انرژی داخلی نمی تواند در تحلیل استاتیکی به انرژی جنبشی تبدیل شود.

اگر بخواهیم تعادل را پیدا کنیم، حلگر Implicit نمی تواند به تنهایی و بدون کمک، پاسخ را پیدا کند. به عنوان مثال با اعمال کردن دمپینگ.

حلگر Explicit همیشه تعادل دینامیکی را حل می کند. یعنی معادله مربوط به تساوی نیرو با حاصلضرب جرم و شتاب. در تحلیل با Explicit ، ارتعاش و نوسان بیشتری نسبت به حالت Implicit وجود دارد. در این حالت، زمان معنای فیزیکی واقعی دارد و نرخ بارگذاری اهمیت بالایی پیدا می کند.

نرخ بارگذاری روی سایز گام زمانی پایدار اثری نمی گذارد.

اگر قرار باشد اثرات دینامیکی در مسئله وارد نشوند، نیرو باید به آرامی اعمال شود تا نیروی ایجاد شده در نتیجه ضرب جرم و شتاب، مقدار چشم گیری نداشته باشد.

یک راه جایگزین برای اینکه نیرو سریع تر اعمال شود، افزایش گام زمانی پایدار با بالا بردن جرم است. به این کار اصطلاحا Mass Scaling گفته می شود که البته می تواند آثار نامطلوب دینامیکی داشته باشد.

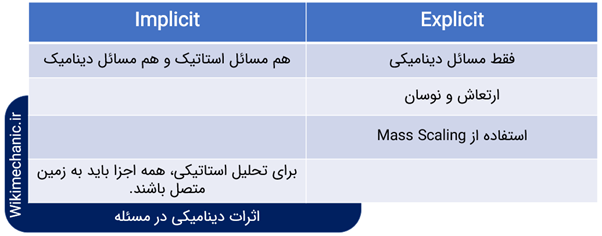
به صورت مختصر و مفید، می توان گفت:

 مسائل تماس و برخورد با Implicit یا Explicit؟

برای حل مسائل تماس (Contact) هم می توانیم از حلگرهای Implicit استفاده کنیم هم از حلگرهای Explicit. در واقع هر دوی این حلگرها، آپشن های مشابهی برای حل مسئله تماس در اختیار ما قرار می دهند.