ب م م اعداد و چند جمله ای ها در متلب

در این قسمت می خواهیم تابعی را برای پیدا کردن بزرگترین مقسوم علیه مشترک یا همان ب م م پیدا کنیم. ابتدا برویم سراغ پیدا کردن ب م م دو عدد در متلب.

به صورت کلی برای بدست آوردن ب م م از تابع gcd در متلب استفاده می کنیم. مثال زیر نشان می دهد که چگونه می توانیم ب م م دو عدد را در متلب محاسبه کنیم.

مثال: می خواهیم بزرگترین مقسوم علیه مشترک دو عدد 128 و 48 را محاسبه کنیم:

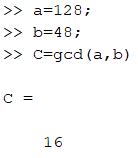
و حتی می توانیم بدون تعریف متغیر این کار را انجام دهیم:

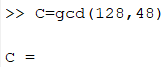
می توانیم این کار را به صورت همزمان برای چند عدد هم انجام دهیم. در این صورت باید اعداد را در دو بردار یا ماتریس همانند مثال زیر وارد کنیم.

مثال: با استفاده از تابع gcd ب م م 4 جفت از اعداد را به صورت همزمان بدست می آوریم. این اعداد را در قالب درایه های دو بردار وارد تابع gcd می کنیم.

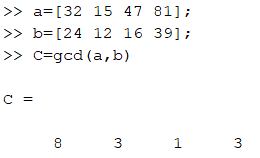
این تابع ب م م درایه های متناظر را محاسبه می کند و به صورت یک بردار با همان ابعاد تحویل می دهد.

دقیقا مشابه مثال بالا می توانیم با استفاده از تابع gcd ، ب م م درایه های متناظر دو ماتریس را هم در متلب محاسبه کنیم.

تا اینجای کار درباره نحوه محاسبه بزرگترین مقسوم علیه مشترک دو عدد صحبت کردیم. اما با استفاده از این تابع می توانیم ب م م دو چند جمله ای را هم در متلب پیدا کنیم. ب م م دو چند جمله ای، بزرگترین چند جمله ای است که پس از تجزیه دو عبارت، در بین آن ها مشترک است.

برای استفاده از این قابلیت ابتدا باید یک متغیر نمادین یا سیمبولیک در متلب تعریف کنیم تا بتوانیم چند جمله ای ها را به متلب معرفی کنیم. مثال پایین را در نظر بگیرید:

مثال: پس از تعریف متغیر x به عنوان یک متغیر سیمبولیک، چند جمله ای های a و b را بر اساس x تعریف می کنیم. سپس آنها را وارد تابع gcd می نماییم.

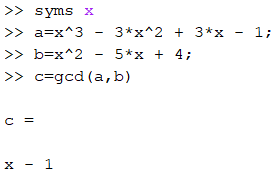
یا اینکه به صورت ساده تر و در یک مرحله بدون تعریف متغیرهای a و b، می توانیم چند جمله ای ها را مستقیم در ورودی تابع gcd بنویسیم.

مثال: این بار عبارت هایی که وارد تابع gcd می شوند، شامل دو متغیر x و y می شوند. این دو متغیر را هم ابتدا با استفاده از syms به عنوان متغیرهای نمادین و سیمبولیک معرفی می کنیم.