محاسبه مقادیر ویژه و بردارهای ویژه یک ماتریس، در حوزه های مختلف کاربردهای فراوانی دارد. بررسی کاربردها را به زمان دیگری موکول می کنیم و در اینجا نحوه محاسبه این مقادیر را با استفاده از نرم افزار متلب شرح می دهیم.

دستور eig در متلب برای پیدا کردن مقدارهای ویژه

فرض کنید ماتریس مربعی A را داریم و می خواهیم مقادیر ویژه این ماتریس را پیدا کنیم. برای این کار کافی است از دستور eig به صورت زیر استفاده کنیم.

البته راه های دیگری هم برای استفاده از دستور eig در متلب وجود دارد که در ادامه به آنها هم اشاره می کنیم.

توجه کنید نام دستور eig در متلب از کلمه eigenvalues  و eigenvectors به معنی مقادیر ویژه و بردارهای ویژه گرفته شده است.

برای آشنایی بهتر با تابع eig در متلب به مثال زیر توجه کنید.

مثال: مقادیر ویژه ماتریس A را که یک ماتریس مربعی 3 در 3 است، محاسبه می کنیم.

همان طور که مشاهده می کنید سه مقدار ویژه برای این ماتریس به دست آمده که دوتا از آنها به شکل مختلط هستند و یکی به صورت حقیقی است.

نکته مهم این است که توجه داشته باشید که برای یک ماتریس مربعی n در n همیشه n تا مقدار ویژه به دست می آید که البته ممکن است تکراری هم باشند.

دستور eig در متلب برای پیدا کردن بردارهای ویژه

از دستور eig متلب می توایم علاوه بر پیدا کردن مقدار ویژه، جهت محاسبه بردار ویژه هم کمک بگیریم. کافیست که دو خروجی برای این دستور تعیین کنیم. در مثال زیر این موضوع کاملا مشخص شده است.

مثال: مقادیر ویژه و بردارهای ویژه ماتریس B را محاسبه کنید.

همان طور که مشاهده می کنید ماتریس B با استفاده از دستور magic در متلب ایجاد شده است. برای به دست آوردن مقادیر ویژه و بردارهای ویژه، دستور eig را به شکل زیر استفاده می کنیم.

در این حالت خروجی اول تابع eig که ما آن را با حرف V نامگذاری کرده ایم بردارهای ویژه را در خود ذخیره می کند و خروجی دوم که با حرف D نامگذاری شده، محل ذخیره سازی مقدارهای ویژه است. یعنی به شکل زیر:

اجازه بدهید کمی توضیح بدهیم. مقادیر ویژه ماتریس B به ترتیب در قطر اصلی ماتریس D قرار گرفته اند. در واقع اگر به صورت ساده تر از دستور   eig استفاده می کردیم همین مقادیر ویژه (ولی این بار در خارج یک ماتریس) نمایش داده می شدند. یعنی به این شکل:

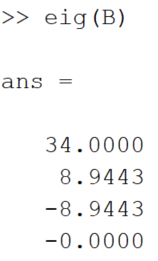
درباره ماتریس مربوط به بردارهای ویژه یعنی همان ماتریس V به این نکته توجه داشته باشید که هر کدام از ستون های این ماتریس یک بردار ویژه را مشخص می کند. از طرفی شماره ستون هر کدام از بردارهای ویژه مشخص می کند که آن بردار با کدام مقدار ویژه متناظر است. در شکل زیر این موضوع به خوبی نشان داده شده است.

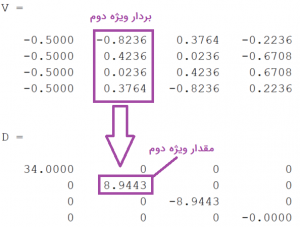
مثلا بردار ویژه موجود در ستون دوم ماتریس، متناظر با مقدار ویژه دوم است. مقدار ویژه دوم هم المان دومی است که در قطر متغیر D وجود دارد. یعنی عدد 8.9443.

پس به این ترتیب با استفاده از دستور eig می توانیم هم مقادیر ویژه و هم بردارهای ویژه را به دست آوریم.