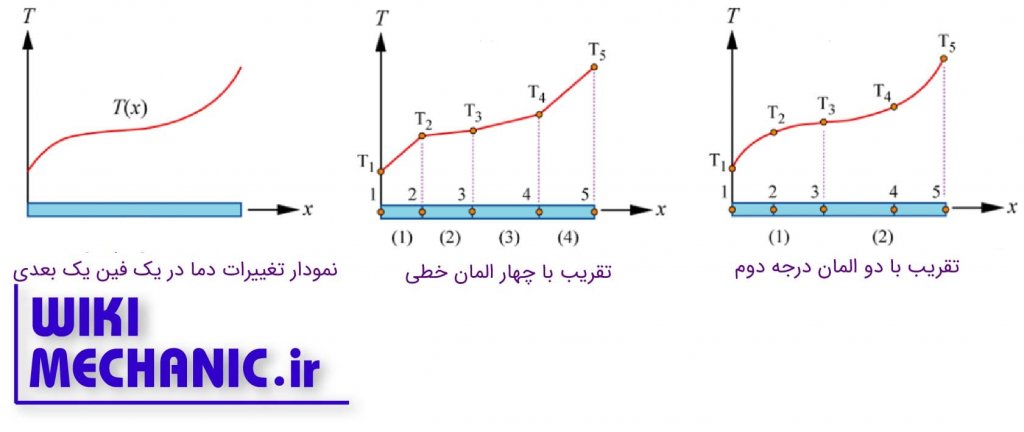
تابع شکل – برای حل مسائل المان محدود، یکی از مهم ترین گام ها انتخاب تابع شکل و به کارگیری درست آن برای حل مسئله است. در گام اول یک تعریف نسبتا سخت از تابع شکل ارائه می دهیم ولی جای نگرانی نیست. چون در ادامه آن را به صورت کامل تشریح می کنیم. تابع شکل در واقع تابعی است که مقدار متناظر با درجه آزادی را در هر گره دریافت می کند و با استفاده از میان یابی، مقادیر آن را در سایر نقاط المان به دست می دهد. پیشنهاد می کنم پیش از این آموزش، المان محدود به زبان ساده را هم مطالعه کنید.
سایر آموزش های مربوط به المان محدود را هم می توانید در این بخش ببینید!
مفهوم درجه آزادی
اولین سوال این است که خب این درجات آزادی که می خواهیم مقدار آنها را به دست آوریم، چه هستند؟
تعریف درجه آزادی: در هر مسئله با توجه به ماهیت آن، تعدادی متغیر وجود دارد که به دنبال به دست آوردن مقادیر آن متغیر در کل دامنه مدل هستیم. مثلا فرض کنید یک پره داریم و می خواهیم مسئله انتقال حرارت مربوط به آن را حل کنیم. بنابراین به دنبال به دست آوردن مقدار دما در هر نقطه از پره هستیم. در اینجا می گوییم «درجه آزادی این مسئله دماست و این مسئله یک درجه آزادی دارد.
حالا فرض کنید یک تیر داریم که تحت خمش است. در هر نقطه مقدار جابجایی (خیز) و شیب برای ما مهم است و باید به دست بیاید. (دقت کنید که برای به دست آوردن تنش و کرنش هم به جابجایی و شیب نیاز داریم.) پس مجهولات یا متغیرهای ما در این مسئله، جابجایی و شیب هستند. در نتیجه می گوییم این مسئله دو درجه آزادی دارد و درجات آزادی آن شیب و جابجایی هستند.
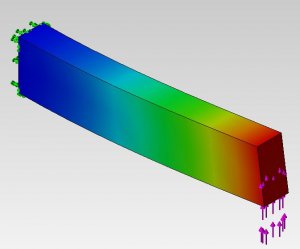
اما نوع درجات آزادی کاملا به تعریف مسئله و خواسته ای که از آن داریم برمی گردد. مثلا همین مثال تیر را در نظر بگیرید. اگر قصد تحلیل تنش و کرنشی داشته باشیم، جابجایی و شیب برای ما مهم هستند و به دنبال آن هستیم که مقدار آنها را در هر نقطه به دست آوریم. اما فرض کنید در همین تیر، به یک طرف آن گرما داده ایم و می خواهیم وضعیت انتقال حرارت در طول آن را بررسی کنیم. در این صورت درجه آزادی دماست. تیر، همان تیر است. ولی در مسئله اول دو درجه آزادی و در مسئله دوم یک درجه آزادی داریم. پس تا اینجای کار، اهمیت «هدف ما از مسئله» را در مشخص کردن درجات آزادی مشاهده کردید.
حالا که با مفهوم «درجه آزادی» آشنا شدید، می توانیم ساده تر درباره هدف از به کارگیری تابع شکل را شرح دهیم. همانطور که گفته شد، در مسئله به دنبال پیدا کردن درجات آزادی در هر نقطه هستیم. اما با استفاده از حل معادلات ماتریسی، فقط مقدار درجات آزادی در گره ها به دست می آید. پس بقیه نقاط مدل که در نقاطی غیر از گره ها و بر روی المان ها قرار دارند چه می شوند؟ مقدار متغیرها و درجات آزادی در آن نقاط چگونه به دست می آید؟ پاسخ این سوال را تابع شکل به ما می دهد. خاصیت تابع شکل این است که با توجه به مقدار درجات آزادی در گره های اطراف یک المان، مقدار آنها را در سایر نقاط المان مشخص می کند. تابع شکل این کار را با استفاده از درون یابی انجام می دهد.
مثال: المان فنر
فرض کنید در المان زیر به دنبال پیدا کردن U1 وU2 یعنی جابجایی در ابتدا و انتهای المان هستیم. با پیدا کردن این دو مقدار و به دست آوردن تفاضل آنها کرنش المان به دست می آید و سپس می توانیم با استفاده از کرنش، تنش را محاسبه کنیم. پس در اینجا درجه آزادی، جابجایی است. فرض می کنیم مقدار جابجایی در داخل هر المان به صورت خطی تغییر می کند. در این صورت در هر المان خواهیم داشت:
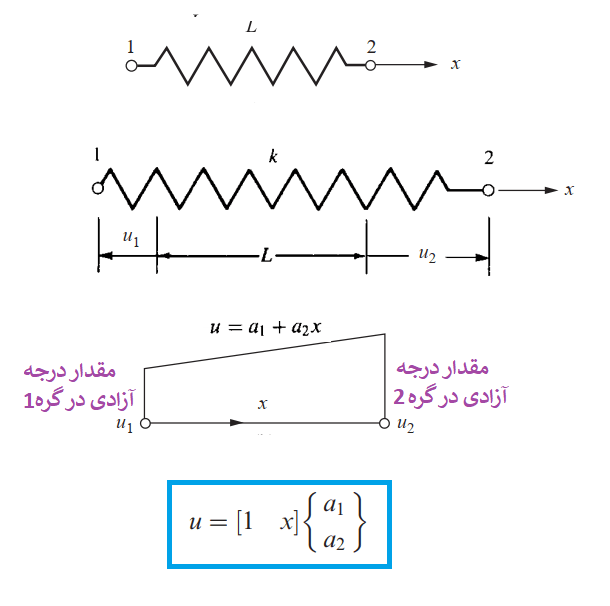
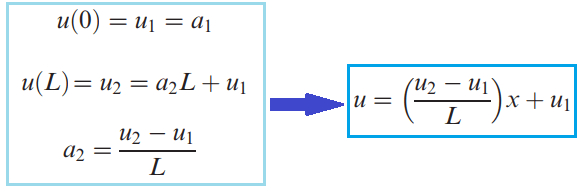
بنابراین ماتریس جابجایی را می توان به صورت زیر و بر حسب جابجایی در گره ها نوشت:
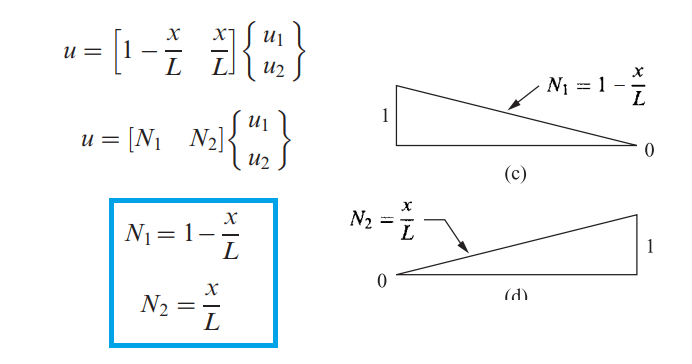
N1 که ضریب درجه آزادی اول است و N2 که ضریب درجه آزادی دوم است، ضرایب شکل نامیده می شوند. با جایگزینی مقادیر 0 تا L در x ، مقدار جابجایی در نقطه x المان بر حسب مقدار جابجایی در نقطه اول و آخر المان به دست می آید. یک ویِژگی مهم تابع شکل که در توابع شکل به دست آمده در مثال بالا هم مشخص است،ِ این است که مقدار تابع شکل در گره مربوط به آن برابر 1 و در سایر گره ها صفر می باشد. مثلا N1 را در نظر بگیرید. در نقطه x=0 (یعنی در محل المان اول) مقدار آن برابر 1 است و در x=l مقدار آن برابر صفر است.
نکته: در اینجا فرض شده که تغییرات در داخل المان خطی است و در واقع تابع شکل درجه 1 است. ممکن است در بعضی مسائل، توابع شکل از نوع دیگری باشند.
به عنوان خلاصه باز هم همان جمله ابتدا را البته کمی مشروح تر تکرار می کنم. در حل مسائل، مقدار درجات آزادی در گره ها به دست می آید. برای اینکه مقدار درجه آزادی در بقیه نقاط هم به دست بیاید، توابع شکل به ما کمک می کنند و با استفاده از مقدار به دست آمده در گره ها، مقدار درجات آزادی را در سایر نقاط هم مشخص می کنند.
مثالی که در این آموزش ارائه شد، ساده ترین مثالی بود که برای تابع شکل وجود داشت. در المان های دیگری که در هر گره بیش از یک درجه آزادی وجود دارد یا گره های بیشتری در یک المان وجود دارد یا شکل المان از حالت یک بعدی ساده خارج می شود، استخراج تابع شکل دشوارتر خواهد بود. به عنوان مثال حالت های زیر را در نظر بگیرید. مثلا در حالتی که سه گره در یک المان موجود باشد، برای اینکه خاصیت تابع شکل (این خاصیت که در گره مربوط به خودش مقدار 1 دارد و در سایر گره ها مقدار 0) برقرار باشد، چاره ای نداریم جز اینکه یک تابع شکل درجه دوم برای آن برگزینیم. چرا؟ به شکل های زیر توجه کنید. آیا در حالت دوم، می توان تابعی خطی پیدا کرد که همزمان مقدارش در دو گره صفر باشد و در یک گره یک باشد؟ طبیعتا امکان پذیر نیست. به دلیل مشابه، وقتی در یک المان چهار گره داشته باشیم باید از تابع شکل درجه سه استفاده کنیم.

حالا به بالا برگردید و سعی کنید تصویری که در ابتدای آموزش گذاشته ام را تحلیل کنید. در آموزش های بعدی، استخراج توابع شکل در حالات دیگر را هم بررسی خواهیم کرد.


