روش های عددی؛ یک راه حل برای شرایط پیچیده

المان محدود به زبان ساده –  پدیده های فیزیکی معادلاتی دارند که بر آنها حاکم است و شرایط آنها را توصیف می کند. این معادلات اکثرا به صورت معادلات دیفرانسیلی هستند و اکثرا هم به دلیل شرایط پیچیده ای که در مدل و محیط اطراف آن وجود دارد به صورت غیرخطی و بسیار پیچیده درمی آیند. در این مواقع روش های معمول تحلیلی که تحت عنوان درس «معادلات دیفرانسیل» ارائه می شوند دیگر قابل استفاده نیستند. بنابراین به روش های دیگری برای حل این معادلات به کار گرفته می شود که روش های عددی نام دارند.

سایر آموزش های مربوط به المان محدود را هم می توانید در این بخش ببینید!

 در روش های عددی الگوریتم های خاصی تعریف می شوند که بارها و بارها روی معادله اعمال می شوند تا جواب تقریبی مسئله به دست آید. دقت کنید این جواب ها تقریبی هستند و همواره مقداری خطا دارند. اما می توان با انجام چندباره الگوریتم های گفته شده، به اندازه مناسبی خطا را کاهش داد و به جواب دقیق مسئله نزدیک شد.

دقت داشته باشید که روش های عددی متعددی برای حل معادلات دیفرانسیل وجود دارند. در بعضی مسائل با توجه به شرایط مرزی داده شده، ممکن است برخی از این روش ها ما را به جواب نرسانند.

و اما المان محدود…

المان محدود (بعضی ها هم می گویند اجزا محدود!) هم یکی از روش های عددی است که از آن می توان برای حل عددی معادلات دیفرانسیل استفاده کرد. در این روش برای ساده سازی مسئله، کل ناحیه ای که در آن باید معادلات حل بشوند، به اجزای کوچکتری تقسیم می شود که هر جزء، یک المان (Element) نام دارد. همانطور که از نام این روش هم پیداست، تعداد المان ها ممکن است زیاد باشد اما محدود (Finite) است و بی نهایت نیست. در واقع می توان المان ها را شمرد. بنابر این ، نام اختصاری این روش FEM است: Finite Element Method

پس هدف اصلی روش المان محدود این است که با استفاده از جایگزینی مسئله با یک مسئله ساده تر، راه حل مسئله را پیدا کند. (فرض های ساده شونده ای در نظر می گیریم که مسئله ساده تر می شود.)

با توجه به این فرض های ساده شونده و تعداد محدود المان ها، طبیعتا دقت حل مساله هم محدود است و به میزان معینی خطا وجود دارد. مثلا 5 درصد، 10 درصد …

یکی دیگر از روش های عددی که برای حل معادلات دیفرانسیل کاربرد دارد، روش تفاضل محدود است که به اختصار به آن FDM گفته می شود: Finite Difference Method . البته روش المان محدود به صورت کلی محبوبیت بیشتری در بین مهندسان دارد. در هر دو روش ابتدا باید معادلات دیفرانسیل حاکم بر سیستم به دست آید. در ادامه حل، در روش اجزا محدود، معادلات دیفرانسیلی موجود را از طریق فرمول های انتگرالی به معادلات جبری و ساده تر تبدیل می کنیم. اما در روش تفاضل محدود، روابط تفاضلی را جایگزین مشتقات موجود در معادلات می کنیم.

یک مثال ابتدایی

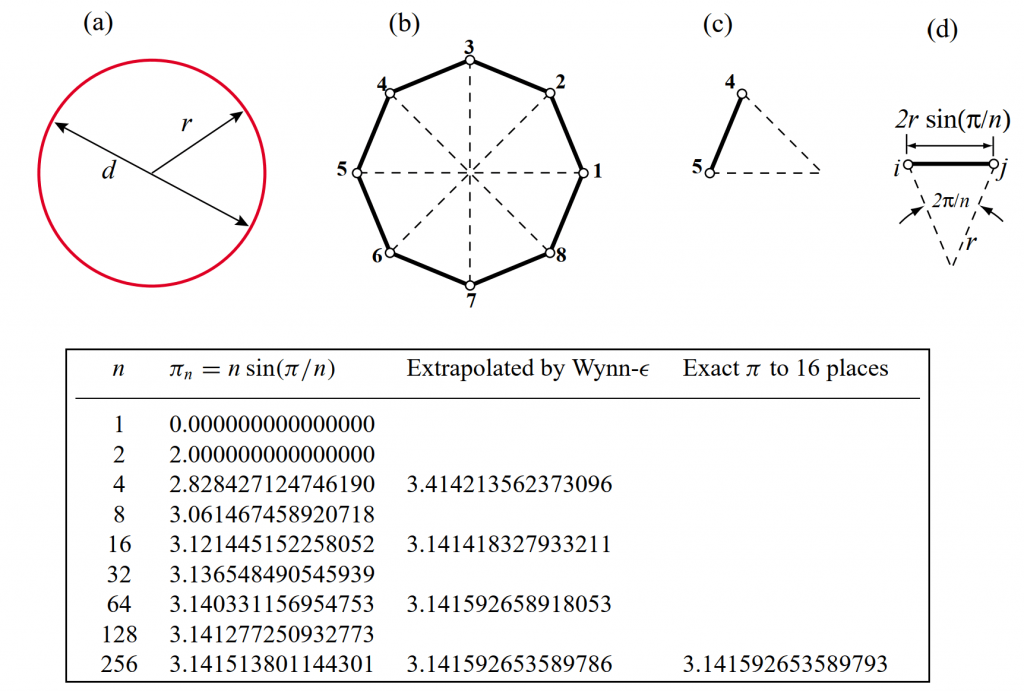
مثال زیر در کتاب «معرفی روش اجزا محدود» نوشته «فلیپا» آورده شده است. هدف از این مثال، به دست آوردن تقریبی مقدار عدد پی است. در این مثال مساحت یک دایره با تقسیم آن به مثلث های کوچکتر و به دست آوردن مساحت این مثلث ها، به صورت تقریبی به دست آورده شده است. هر کدام از این مثلث ها یک المان هستند. پس از به دست آوردن مساحت، مقدار عدد  به صورت تقریبی به دست آورده شده است. همانطور که مشاهده می کنید با افزایش تعداد المان ها (n) مقدار به دست آمده برای عدد «پی» دقیق تر می شود.

رویکردهای حل مسئله المان محدود

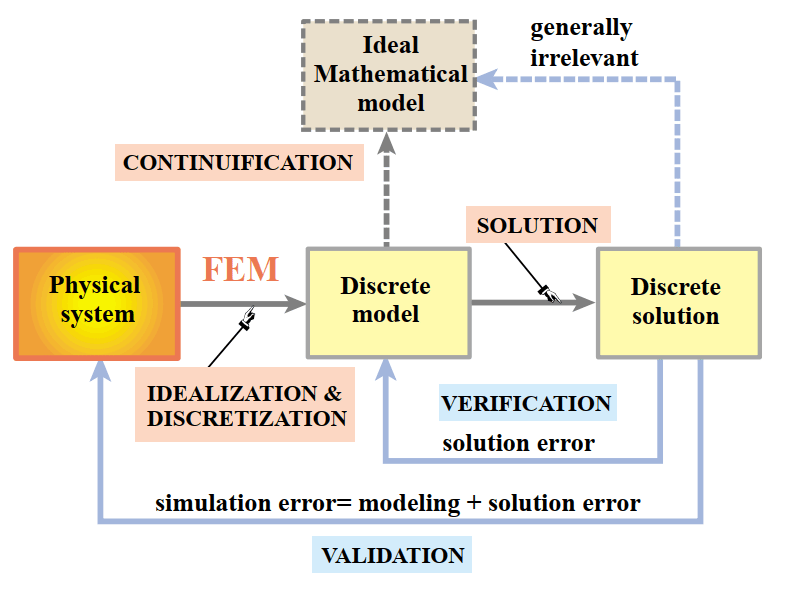
نمودارهای زیر دو رویکرد ریاضیاتی و فیزیکی را در حل مسائل با استفاده از FEM نشان می دهد. در روش اول، ابتدا با استفاده از ساده سازی از روی مدل فیزیکی یک مدل ریاضی تشکیل می دهیم. این مدل ریاضی باید بتواند کلیت سیستم را به خوبی توصیف کند. ممکن است بپرسید چرا باید مدل ریاضی ایجاد شود؟ چرا با همان مدل فیزیکی ادامه نمی دهیم؟ پاسخ این است که روش های علمی برای تحلیل ها، همگی مبتنی بر ریاضیات هستند و برای مدل فیزیکی صرف، راهکاری ندارند.

بعد از ایجاد مدل، همانطور که در شکل مشاهده می کنید، نوبت به گسسته سازی و تقسیم به المان های کوچک تر می رسد. پس از آن معادلات مربوط به المان ها حل می شود. پس از حل معادلات باید پاسخ به دست آمده به صورت فیدبک با نتایج حاصل از مراحل قبلی مقایسه شود. نتایج با مدل فیزیکی واقعی، مدل ریاضی و مدل گسسته مقایسه می شود و در صورت تناقض، تدابیری برای اصلاح ایرادات اتخاذ می شود. نرم افزارهای حوزه FEM نظیر آباکوس و انسیس، در این مرحله و برای حل این معادلات ریاضی به ما کمک می کنند. البته در صورتی که ساده سازی ها را خودمان انجام نداده باشیم، این نرم افزارها باز هم به ما کمک می کنند که در ادامه توضیحات لازم را آورده ایم.

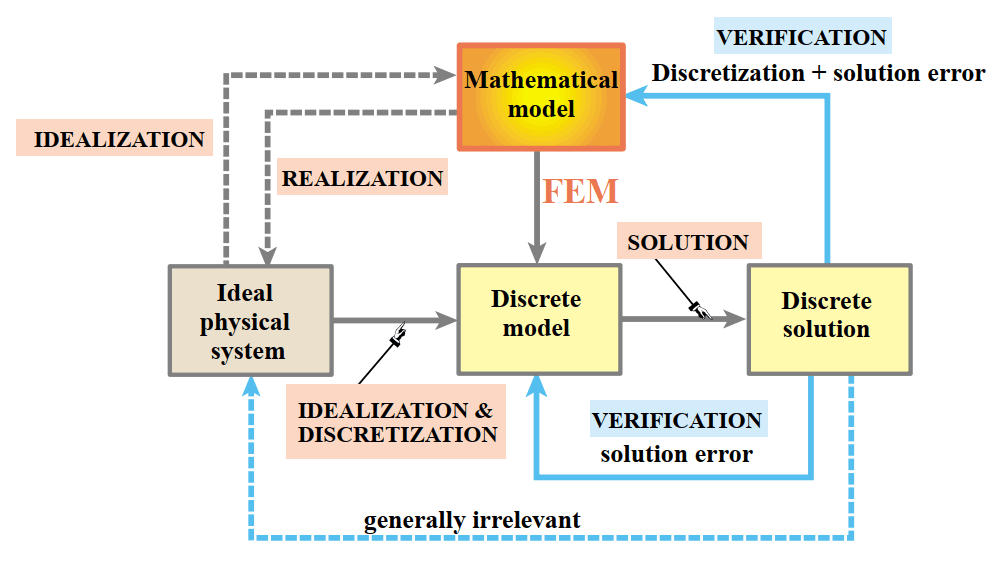
رویکرد دوم به این شکل است که فرایند FEM به صورت مستقیم بر روی مدل فیزیکی انجام می شود. در واقع در نرم افزارهایی که بر پایه المان محدود کار می کنند ( مانند آباکوس، انسیس، کامسول و …) از این رویکرد تبعیت می کنند. در واقع این نرم افزارها کار ما را ساده می کنند. ساده شدن کار از این جهت است که دیگر نیازی به ایجاد مدل ریاضی نیست و مستقیما مدل فیزیکی به نرم افزار داده می شود. البته باز هم بهتر است تا حد ممکن ساده سازی در مدل انجام شود تا سرعت حل افزایش یابد.

مراحل انجام روش المان محدود

نخستین گام، ساده سازی و ایده آل سازی  مسئله است. اما منظورمان از ایده آل سازی چیست؟ برای درک بهتر این موضوع، به تصویر زیر دقت کنید. تصویر بالایی یک سازه را نشان می دهد که وجود خارجی دارد. اما برای تحلیل آن باید این سیستم فیزیکی ساده سازی شود. همانطور که مشاهده می کنید تصویر پایینی، شکل ساده شده سازه را نشان می دهد. یعنی: از وزن مفصل ها صرف نظر شده، وزن اجزا به طور مساوی در مفاصل کناری تقسیم می شود و …

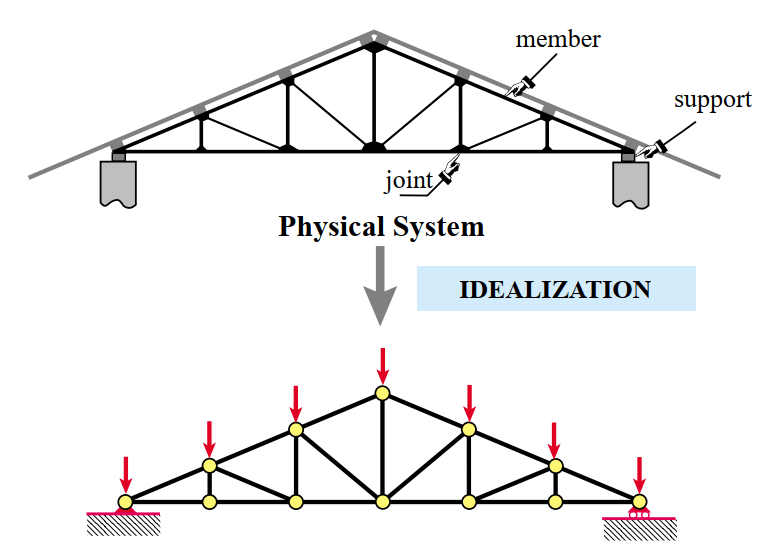
همه این ساده سازی ها باعث می شود حل کلی مسئله به شدت ساده تر شود. البته ساده سازی نباید طوری باشد که اصل مسئله دچار تغییرات زیاد شود و از مسئله اصلی فاصله بگیرد.

ساده سازی در مسائل مختلف متفاوت است و در هر مسئله روش های خاص خود را دارد.  بخش زیادی از این روش ها از طریق تجربه کسب می شود. مثال خرپای بالا صرفا یک مثال ساده است. در موارد پیچیده تر ممکن است همین ساده سازی بسیار دشوار شود.

گام دوم تقسیم مدل به المان های کوچک تر است. در مسئله بالا هر یک از میله های خرپا به عنوان یک المان در نظر گرفته می شود. در مسائل سخت تر، انتخاب نوع المان و تعداد المان ها ممکن است یک چالش باشد.

پس از ساده سازی و درک نوع مسئله و معادلات حاکم بر سیستم، نوبت به انتخاب تابع شکل مناسب (Shape Function) می رسد.  تابع شکل در واقع تابعی است که با توجه به نوع مسئله و نوع المان های انتخاب شده به دست می آید. هر مسئله یک تابع شکل دارد که به حل معادله دیفرانسیل مربوط به آن مسئله کمک می کند. کارکرد مهم تابع شکل این است که با توجه به مقدارهای به دست آمده در گره ها (گره ها در ادامه همین مقاله معرفی شده اند)، مقدار پارامتر مورد نظر را در طول المان درون یابی می کند.

یعنی چه؟! فرض کنید متغیر ما (یا همان درجه آزادی) در یک مسئله ، دما باشد. تابع شکل با توجه به مقدارهایی که برای دما در گره ها به دست آمده است، مقدار دما در سایر نقاط هر المان را به دست می دهد. برای آشنایی بیشتر با تابع شکل و نحوه به دست آوردن توصیه می کنم حتما مقاله ای را که درباره آن نوشته ایم مطالعه کنید. در آن مقاله برای درک بهتر تابع شکل، مثال هم زده شده است : تابع شکل؛ یکی از پایه های المان محدود

در گام بعدی باید ماتریس سختی را بدست آوریم. درایه های ماتریس سختی، با توجه به نوع مسئله ( اینکه مسئه انتقال حرارت باشد یا تنش کرنش باشد یا …) متفاوت است اما روش و رویکردی که برای بدست آوردن آن استفاده می شود، یکسان است.

پس از طی این مراحل، نوبت به این می رسد که شرایط مرزی و بارگذاری ها را تاثیر بدهیم. مثلا درباره خرپای زیر، شرایط مرزی حکم می کند که انتهای سمت راست آن در راستای عمودی جابجایی نخواهد داشت (چون تکیه گاه غلتکی دارد.). همچنین انتهای سمت چپ آن هیچ گونه جابجایی در راستاهای افقی و عمودی ندارد. در هنگام ساده سازی مسئله باید به این نکته توجه داشته باشید که تا جای ممکن، شرایط مرزی دچار تغییر نشوند.

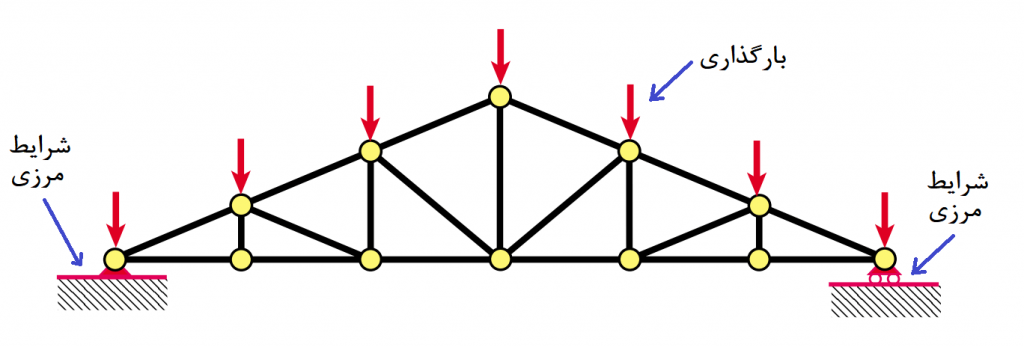
با مفهوم المان آشنا شدید. مفهوم مهم دیگری نیز وجود دارد به نام «گره» یا همان Node. گره به محل اتصال یک یا چند المان به یکدیگر گفته می شود. در شکل زیر المان ها و گره ها مشخص شده اند.

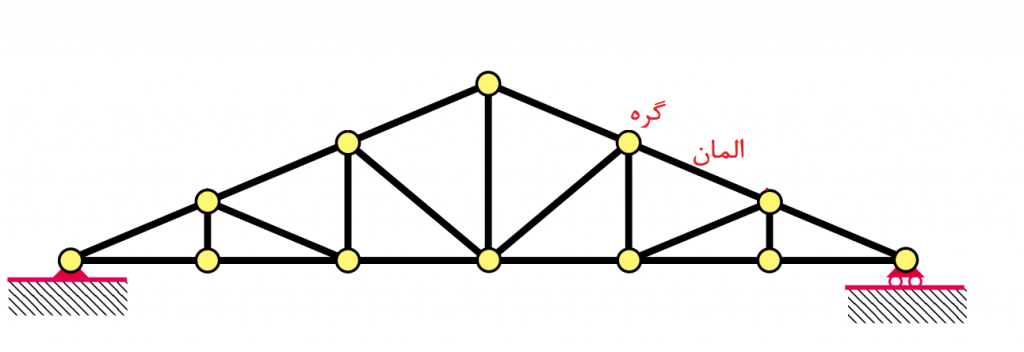
هر المان شامل مقداری اطلاعات است. اطلاعات این المان ها از طریق گره ها، با هم ارتباط پیدا می کنند و باعث می شوند که مسئله روند حل مناسبی را طی کند. با یک مثال، منظور جمله قبلی مشخص می شود. فرض کنید مسئله خیز تیر را می خواهیم حل کنیم. فرض کنید مقدار خیز در یک المان برابر در حوالی 1.5 میلی متر به دست می آید. (چرا می گوییم «در حوالی» ؟ چون مقدار خیز تیر یا هر یک از متغیرهای دیگر، در همه جای یک المان الزاما ثابت نیست و تغییر می کند.) وجود گره ها باعث می شود که المان های کناری با این المان در ارتباط باشند و مقادیر بی ربطی (مثلا 50 میلی متر!) برای آنها به دست نیاید.